Ученые нашли точное решение для класса сложных инженерных задач, впервые использовав соотношение ортогональности Папковича вместо обычно применяемого интегрального преобразования Фурье. Статья опубликована в журнале Mathematics and Mechanics of Solids. Исследования поддержаны грантом Президентской программы Российского научного фонда (РНФ).
Чтобы избежать трещин, деформаций и разрушения элементов сложных конструкций, инженерам необходимо учитывать то, как объект поведет себя при нагрузке. Это, в свою очередь, требует сложнейших математических расчетов при проектировании. Один из открытых вопросов инженерии связан с решением прикладных задач для того случая, когда нагрузка приложена не на границах, а внутри области. Такие случаи называются неоднородными краевыми задачами теории упругости. В них нужно найти точные решения неоднородных дифференциальных уравнений в частных производных, удовлетворяющие тем или иным условиям на границе области. Одна из таких задач — передача нагрузки от упругого элемента, расположенного внутри области, к тонкому листу. На практике она реализуется, например, при взаимодействии стрингера (продольный элемент каркаса) самолета и его обшивки.
«В 60-80 годы прошлого столетия этим задачам уделялось огромное внимание многих выдающихся ученых, но сейчас их работы в значительной степени забыты. Отчасти это связано с тем, что формулы, описывающие решение, достаточно сложны и требуют от исследователя значительных математических навыков. Вторая и главная причина состоит в том, что все решения были приближенными. Поэтому от статьи к статье подходы сильно отличались, что сказывалось и на результатах», — рассказывает руководитель проекта по гранту РНФ Александр Кержаев, кандидат физико-математических наук, старший научный сотрудник Института теории прогноза землетрясений и математической геофизики РАН.
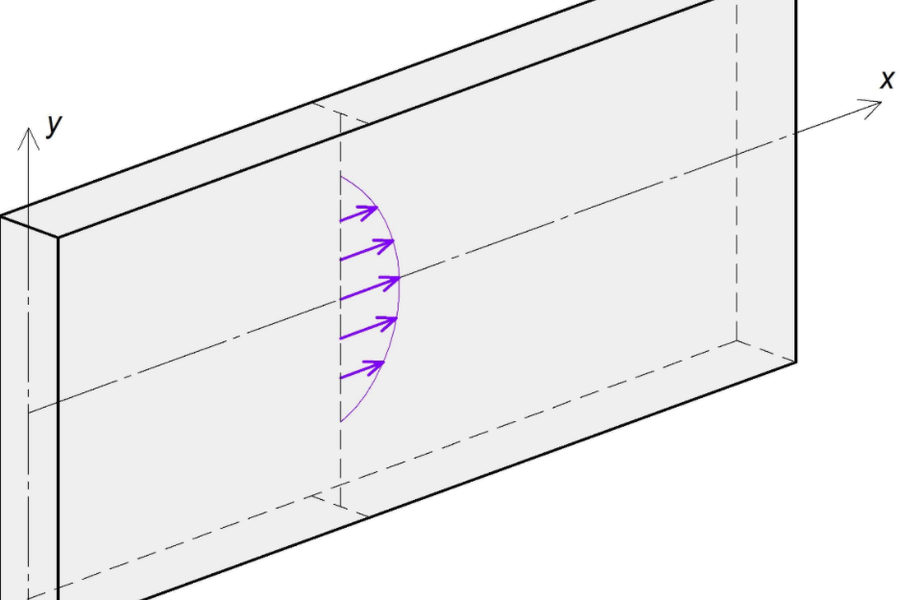
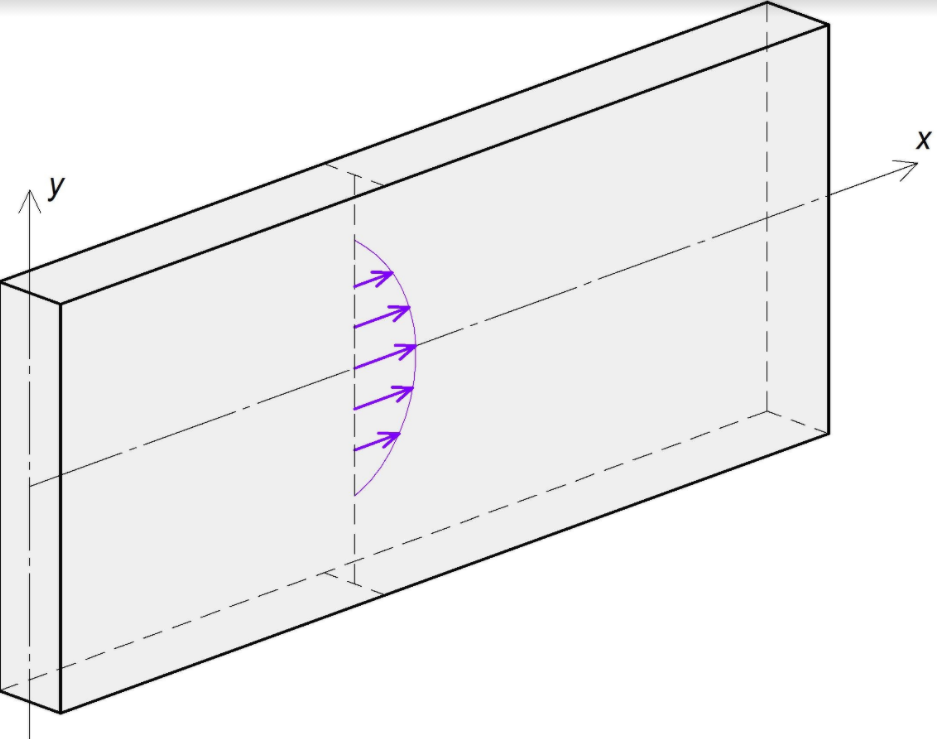
Ученые из Института теории прогноза землетрясений и математической геофизики РАН (Москва) предложили метод построения точных решений неоднородных задач теории упругости в полуполосе. С точки зрения инженерии полуполосой является прямоугольник, у которого длина значительно больше ширины — например, достаточно длинная бетонная балка. Закрепим эту балку горизонтально, полагая, что внутри нее действует массовая нагрузка, передаваемая к ней через металлический каркас. Концы этой балки могут быть, например, свободными или жестко закрепленными. Для безопасности и долговечности конструкции необходимо знать, как внутри нее распределяются напряжения. Точное решение этой задачи всегда представляло большой прикладной и теоретический интерес.
Предложенный учеными метод построения состоял в следующем: вначале они решили неоднородную задачу для бесконечной полосы, впервые применив для этого соотношение ортогональности Папковича. Затем к нему добавили соответствующее решение однородной задачи для полуполосы (полученное авторами ранее), с помощью которого удовлетворяются граничные условия на торце. Использование соотношения ортогональности вместо классического способа — интегрального преобразования Фурье — быстро приводит к цели. Полученное решение является точным, так как коэффициенты разложений в ряды по собственным функциям Папковича–Фадля определяются в явном виде. Это решение базируется на принципиально новом математическом аппарате, разработанном авторами в предыдущих работах. Ученые продемонстрировали метод на примерах точных решений двух неоднородных краевых задач теории упругости для полуполосы со свободными длинными сторонами. В первом случае торец полуполосы свободен, а во втором он жестко защемлен.
«Соотношение ортогональности Папковича остается справедливым и для других типов однородных граничных условий на сторонах полосы, в частности, когда ее стороны жестко защемлены. Поэтому данным методом можно находить простые точные решения для широкого круга неоднородных краевых задач в полосе с различными однородными граничными условиями на ее длинных сторонах. Эти решения также будут представляться рядами по собственным функциям Папковича–Фадля», — прокомментировал Александр Кержаев.

 Цивилизация
Цивилизация